Videti je preprosta enačba, ki bi jo znal rešiti vsak osnovnošolec, a očitno ni tako. Vsake toliko časa se, včasih s temi številkami, včasih s kakšnimi drugimi, pojavi na socialnih omrežjih in skoraj vedno sproži neskončne debate o tem, kaj je prava rešitev. Je 9 ali 1? No, dajmo zadevo razrešiti enkrat za vselej.
V matematiki obstaja pravilo glede vrstnega reda operacij. Najprej vedno rešimo oziroma se znebimo oklepajev, nato potenc/korenov, sledi množenje in deljenje in na koncu seštevanje in odštevanje. Kaj pa, če si sledijo enakovredne operacije? Takrat gremo lepo po vrsti od leve proti desni. Če bi vam nekdo rekel, naj izračunate enačbo 7 + 6 × 5 =… z njo verjetno ne bi imeli težav. Ker veste, da ima množenje prednost, boste najprej zmnožili 6 x 5, nato dodali 7 in dobili 37.
In zakaj je potem zgornja enačba tako problematična? Ker obstajata dve »interpretaciji«.
Po prvi (pravilni) je postopek tak, da najprej rešimo oklepaj:
6 : 2(1+2) = 6:2(3)
Ker je sedaj v oklepaju le eno število, ki je pozitivno, lahko oklepaj preprosto izpustimo in dobimo:
6 : 2 x 3 =
Od tud naprej imamo pravzaprav dve pravilni poti. Prva je ta, da enačbo obravnavamo od leve proti desni, saj sta deljenje in množenje enakovredni operaciji:
6 : 2 = 3 in 3 x 3 = 9
Druga možnost je, da deljenje pretvorimo v množenje, s tem dobimo same enake operacije in je zaradi tako imenovane komutativnosti (5 x 4 = 4 x 5) vrstni red množenja nepomemben:
6 : 2 x 3 = 6 x 1/2 x 3 = 3 x 3 ali 6 x 3/2 = 9
In v čem je potem težava? V izrazu 6 : 2 x 3 = oziroma v znaku za deljenje. Deljenje dveh, števil, imenujmo jih levo (L) in desno (D) poteka tako, da L delimo z D, kar zapišemo z L : D = L/D. In kaj je v izrazu 6 : 2 x 3 = je L in kaj D? Če je L število 6, potem mora biti D seveda 2 x 3, kar je seveda 6 in rezultat je:
6 : 2(3) = 6 : (2 x 3 ) = 6 / 6 = 1
Od kod takšna logika? Vzemimo, da v izrazu 6 : 2(3) namesto 6 pišemo x, namesto 3 pa y. Dobimo izraz:
x : 2y = x / 2y =
V izrazu je nekako intuitivno, da moramo najprej izračunati 2y nato pa x deliti z rezultatom, mar ne? In če to naredimo, dobimo:
x / 2y = 6 / (2x3) = 6/6 = 1
In kaj je tu narobe? Seveda to, da smo množenju dali prednost pred deljenjem, kar ni prav, saj sta operaciji obratni (deljenje je množenje z obratno vrednostjo) in zato enakovredni, enakovredne opearcije pa vedno obravnavamo po vrsti od leve proti desni.
Katera rešitev je prava?
Če ste uporabnik kakšnega socialnega omrežja, potem ste zagotovo naleteli na tale »problem«.
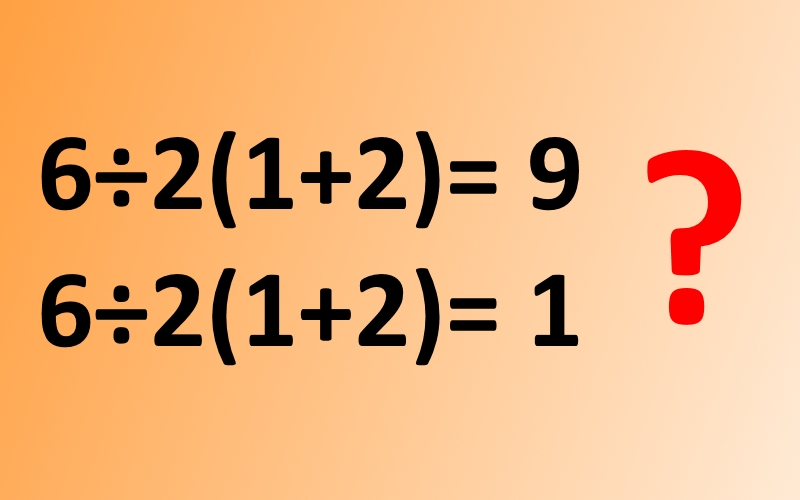
TOP 5 meseca
-
Ekstraktor sperme

Napravo, prvič predstavljeno pred petimi leti, že uporabljajo v praksi.
-
Kaj pa vi slišite?

Po internetu že nekaj časa kroži zvočni posnetek, za katerega se ne ve ali glas v njem reče »Yanni« ali »Laurel«. In spet se je našel razlog za kreganje…
-
»Najboljša odločitev doslej!!«

Avstralka se je pri 38 letih preselila v dom za upokojence. Trdi, da je bila selitev najboljša ideja, kar jih je kdaj sprejela.
-
Simpatične, a jih nihče ne mara...

Ljubke ptičice, ki pa naredijo izredno veliko škode…Ni čudno, da jim »pernate kobilice«...
-
Je pitje vode res tako zdravo?

V nekaterih primerih je, v drugih pa...