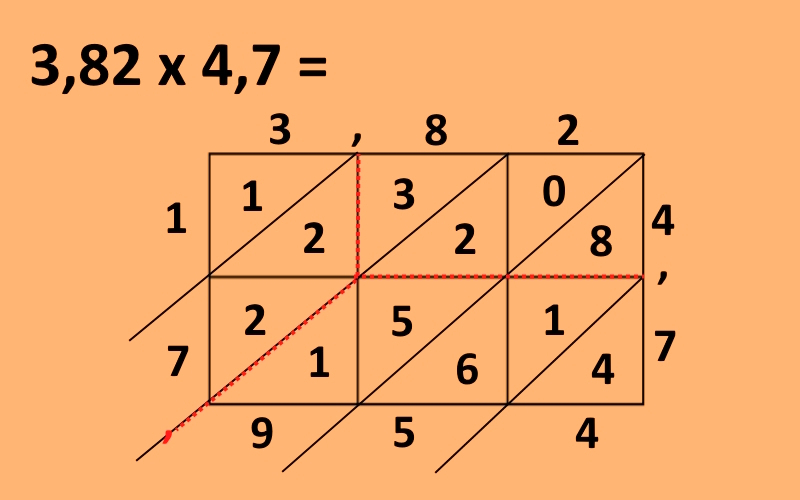
Če vam je klasična metoda, ki ste se jo učili v osnovni šoli, delala težave, si oglejte tole, ki ima svoje temelje v vedski matematiki. Pa jo opišimo kar na prejšnjem primeru množenja 3,82 · 4,7.
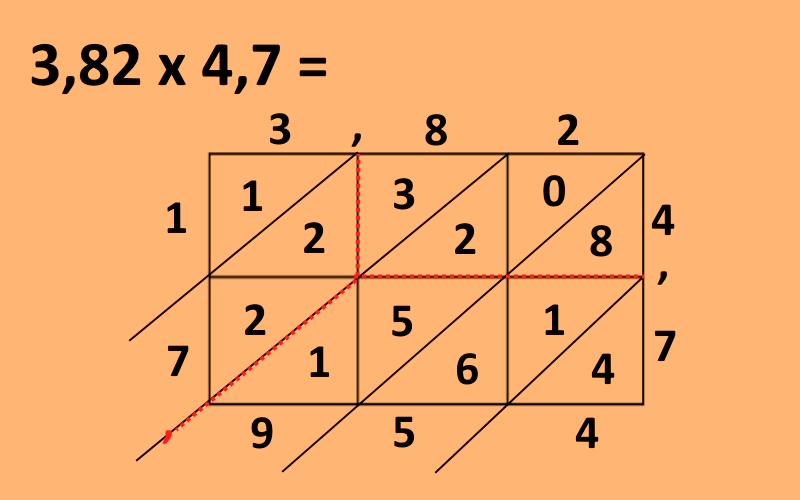
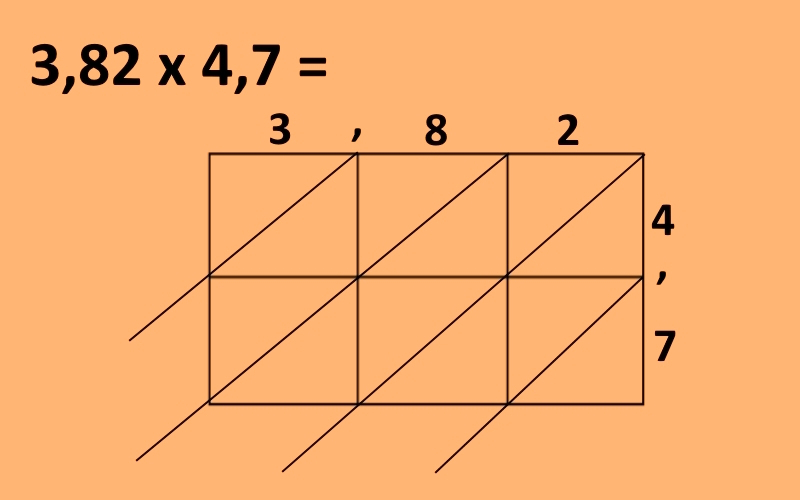
Najprej narišemo pravokotnik in ga črtami razdelimo tako, da ima toliko stolpcev, kot ima števk prvo število in toliko vrstic, kot ima drugo. V našem primeru bo to pravokotnik, ki bo imel tri stolpce in dve vrstici. Nato nad zgornje kvadratke vpišemo prvo število (v napšem primeru 382), ob desne pravokotnike pa drugo (v našem primeru 47), decimalne vejice pa postavimo nad mejnimi črtami med pravokotniki (če decimlanih vejic ni, jih pač ni). Sedaj vse manjše kvadratke oziroma pravokotnike po diagonali razdelimo na dva dela, črte pa podaljšamo tako, da spodaj in levo malce malce štrlijo ven. Dobimo torej nekaj takega.
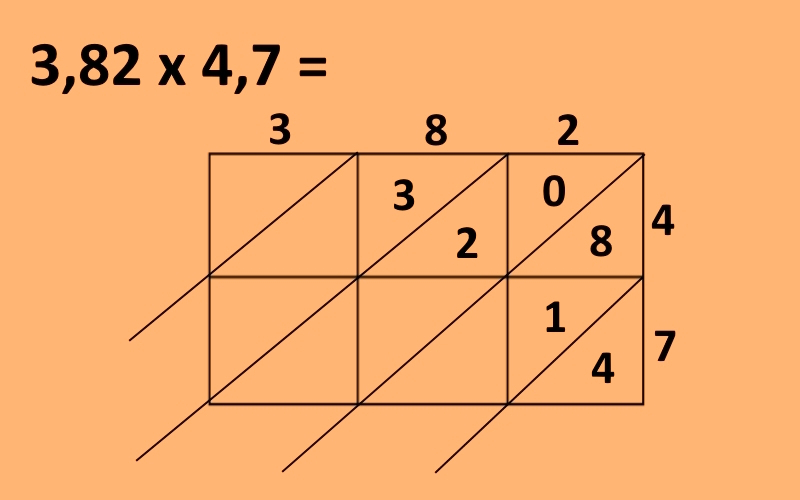
Nato pričnemo števke množiti med seboj in vpisovati v trikotnike, ki smo jih dobili, pri čemer je čisto vseeno, kje začnemo. Vpisujemo tako, da je v posameznem kvadratku v zgornjem trikotniku število desetic, v spodnjem pa število enic. Če začnemo recimo v desnem zgodnjem kotu, moramo v prvi kvadratek torej vpisati rezultat množenja 2 · 4, kar je 8. Ker je število desetic v tem primeru 0, v zgornji trikotnik vpišemo ničlo, v spodnjega pa 8. Postopek nato nadaljujemo. Desno spodaj moramo množiti 2 · 7, kar je 14, torej v zgornji trikotnik vpišemo 1 v spodnjega pa 4.
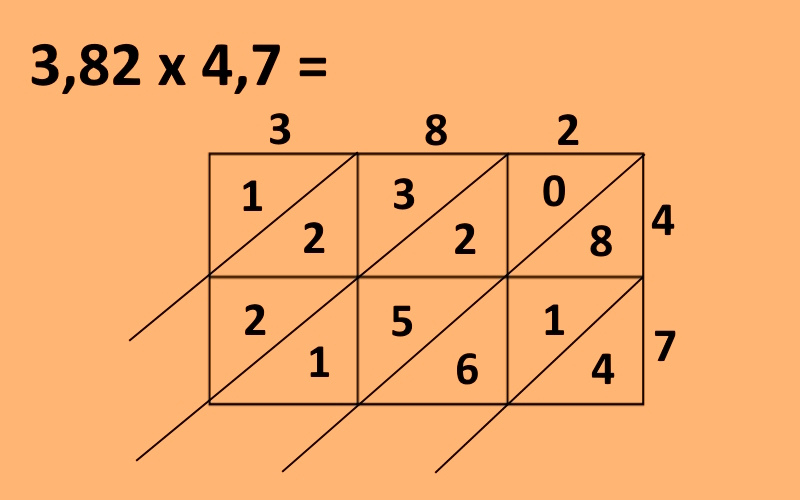
Postopek nato nadaljujemo, dokler ne zapolnimo vseh trikotnikov.
Naslednji korak je preprosto seštevanje, kjer vrednosti seštevamo po diagonalah. Začnemo desno spodaj, kjer imamo samo štirico, torej jo kar prepišemo. V naslednji diagonali imamo števila 8, 1 in 6, kar znese skupaj 15. V prostorček vpišemo petico, enko pa si zapomnimo in jo prenesemo v naslednje seštevanje, ki je 0 + 2 + 5 + 1 in ko dodamo še preneseno enico, dobimo 9, Naslednja diagonala je 2 + 2 +3, kar je skupaj 9, levo zgoraj pa imamo samo enko, ki jo prepišemo. Če zdaj preberemo številke v smeri od levo zgoraj navzdol in potem desno vidimo, da dobimo rezultat 17954, kar je rezultat množenja, če decimalne vejice ne bi bilo, torej če bi množili 382 in 47.
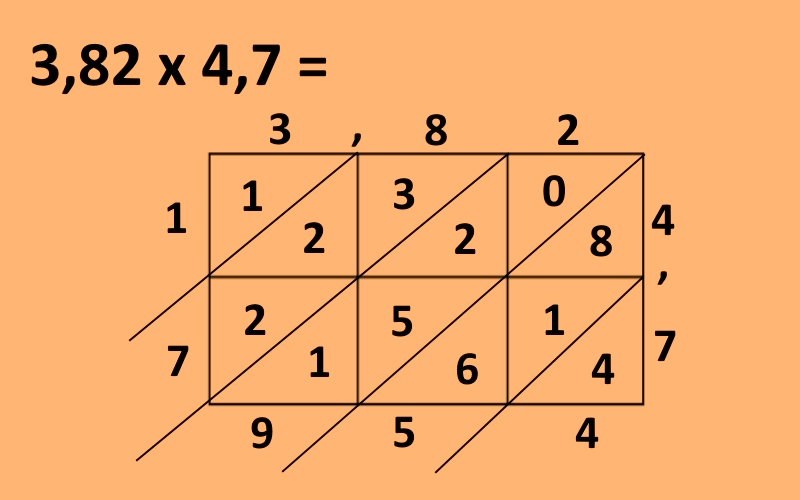
Kaj pa decimalna vejica? Pri tem računu jo je seveda mogoče postaviti kar ročno, saj vemo, da je »nekaj manj kot 4« pomnoženo z »nekaj manj kot 5« enako »nekaj manj kot 20«, pri bolj zapletenih pa se lahko tudi zmotimo. Zato obstaja bolj varna metoda. Ogledamo si črti, nad oziroma ob katerih sta decimalni vejici (zato smo zapisali, da jih zapišemo nad črte). Poiščemo točko, kjer se črti sekata (v našem primeru v desnem spodnjem robu prvega kvadratka) in od tam sledimo diagonali navzdol, dokler ne pridemo do meje med dvema števkama. In tja je potrebno postaviti decimalno vejico.
Vsekakor zabaven in uporaben trik. ▪