Prvo zaporedje je poimenoval »Leti, naravnost, presneto«. Zakaj? Zato, ker njegov graf spominja na sceno iz filma Avatar, v kateri se je glavni junak Jake Sully učil letenja na leteči zveri, imenovani banshee. Najprej je imel težave, nato pa mu je le ratalo leteti v želeni smeri. In prav tak je tudi graf tega zaporedja - najprej se obnaša dokaj čudno, nato pa »pride k sebi« in postane prav simpatičen.
In kakšno je to zaporedje? Prva dva elementa sta 1, nato pa začne veljati pravilo:
a(n) = a(n-1)+n+1 – v primeru, ko števili nimata skupnega delitelja oz. D(n, a(n-1))=1
a(n)= a(n-1)/ D(n, a(n-1)) – v primeru, da števili imata skupnega delitelja oz. D(n, a(n-1))=1 >1
Sliši se zapleteno, a ni tako hudo. V bistvu primerjamo zaporedno število člena in prejšnjo vrednost. Če števili nimata skupnega delitelja, seštejemo prejšnjo vrednost, novo zaporedno število in dodamo 1. Vzemimo primer petega elementa. Predhodno izračunana vrednost četrtega elementa je bila 2. Primerjamo 5 in 2 in ugotovimo, da nimata skupnih deliteljev, zato bo peta vrednost zaporedja 2 + 5+ 1, kjer je 2 prejšnja vrednost, 5 pa novo zaporedno število. Če pa števili imata skupne delitelje, poiščemo največjega in prejšnjo vrednost delimo z njim. Primer je šesti element. Za petega smo izračunali, da je 8, torej moramo primerjati 6 in 8. Števili imata skupnega delitelja, to je 2, zato je rezultata 8/2=4.
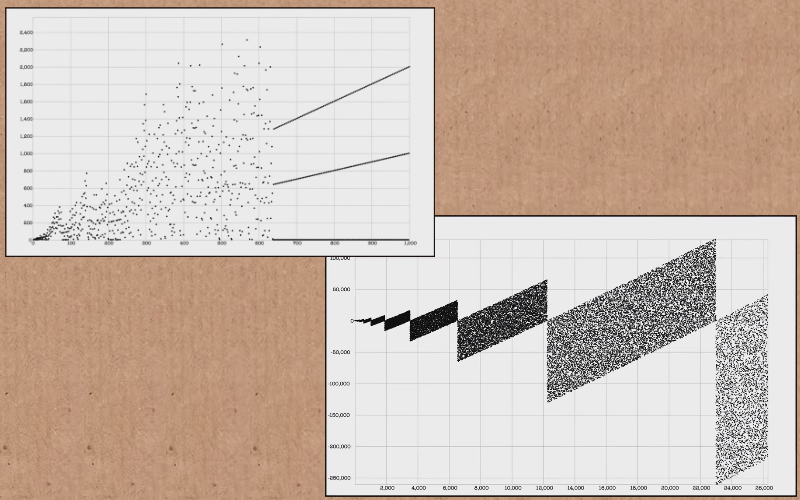
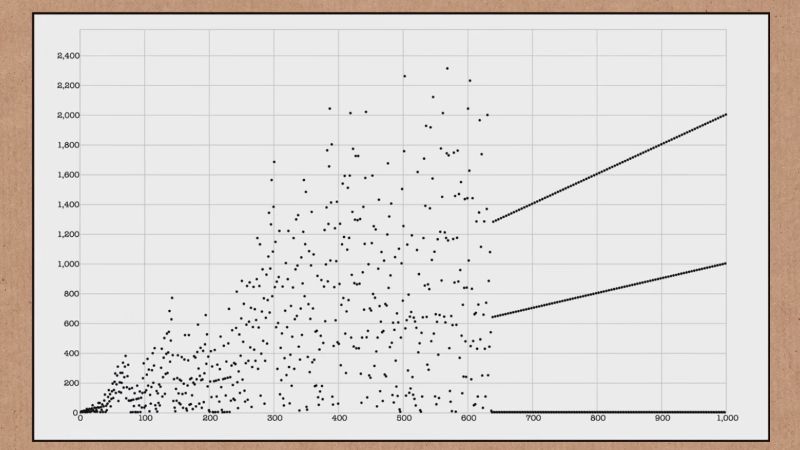
Če člene zaporedja začnemo risati v grafikon vidimo, da so dokaj kaotično »razmetana« naokoli. A le do 638. člena. Takrat se zgodi nekaj zanimivega – graf se »umiri« in nadaljuje s tremi lepimi premicami. Zakaj? Zakaj je člen 638 tako pomemben? Zakaj tri premice? Razloge boste našli v zgornjem videu.
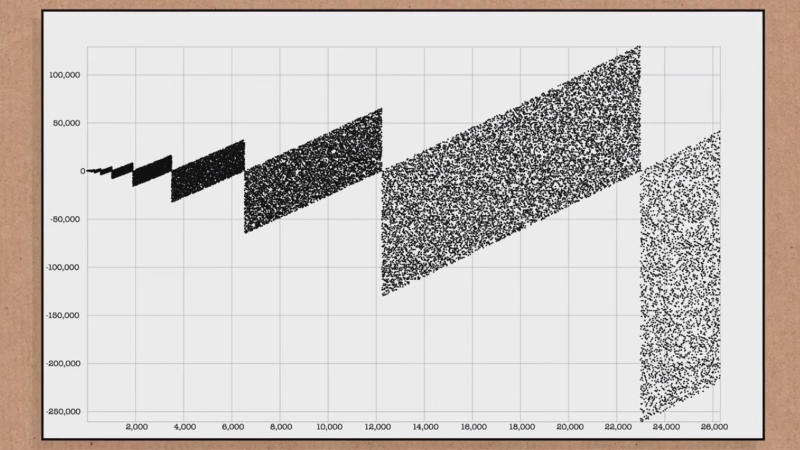
Kaj pa drugo zaporedje? Pri njem se »sprehajamo« med praštevili, člene pa izračunamo tako, da vzamemo praštevilo, ga spremenimo v binarni zapis, tega obrnemo, spremenimo nazaj v desetiškega, število, ki ga dobimo, pa odštejemo od osnovnega praštevila. Spet se sliši bolj zapleteno, kot v resnici je. Vzemimo prvo praštevilo, torej 2. V binarnem zapisu se to glasi 10, obrnjeno 01, kar daje 1 in naslednji člen je zato 2-1=1. Kaj pa recimo 11? Binarno je 1011, obrnjeno 1101, kar je 13, 11-13=-2. In tako naprej. In kakšen je graf tega zaporedja? Je vrsta paralelogramov, ki jih razpolavlja os x, pri čemer je meja med dvema paralelogramoma pri praštevilih, ki so tik pod potenco števila 2. Tak primer je recimo pri 2039, ki je praštevilo, najbližje 2048, torej 211. Vrednost zaporedja v njem je 120, pri naslednjem praštevilu, 2053, pa -508. Tudi to zaporedje je opisano v spodnjem videu, če hočete »skočiti« neposredno nanj, lahko to naredite preko te povezave.
Seveda se spet vprašamo, kaj nam bodo takšna zaporedja oziroma kako so uporabna v praksi. Tako kot pri Van Eckovem zaporedju se tudi tu zaenkrat še ne ve, kar je seveda izziv, ki se ga matematiki veselijo
Vir. Numberphile