Kovinski rez

Pred tednom dni smo pisali o čarobnosti zlatega reza. A ta ni edini magični rez, ki ga poznamo. Obstajajo še drugi. Recimo srebrni. A najprej malo uvoda.

Pred tednom smo zapisali, da Zlati rez dobimo kot »razmerje oziroma delitev neke daljice na dva neenaka dela tako, da je razmerje dolžine daljšega dela proti krajšemu enako kot razmerje dolžine celotne daljice proti daljši«. Takrat smo zapisali, da je definicij in izračunov še kar nekaj. Eden je recimo tudi s pomočjo Fibonaccijevega zaporedja, ki ga dobimo tako, da seštejemo dve predhodni števili. Začnemo z 0 in 1 in nadaljujemo tako, da ju seštejemo. Dobimo 1, nato seštejemo 1 in 1, dobimo 2, nato 2+1=3 in tako naprej. Dobimo zaporedje:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ....

To zaporedje ima lastnost, da dlje kot gremo z njim naprej, bolj se razmerje med dvema zaporednima številoma bliža zlatemu rezu 1,61803….

To vidimo že v teh nekaj zapisanih številih:

3/2=1,5
8/5=1,6
21/13=1,615
55/34=1,617
…
987/610=1,618

Če bi šli še dlje, bi se Zlatemu rezu še bolj približali.

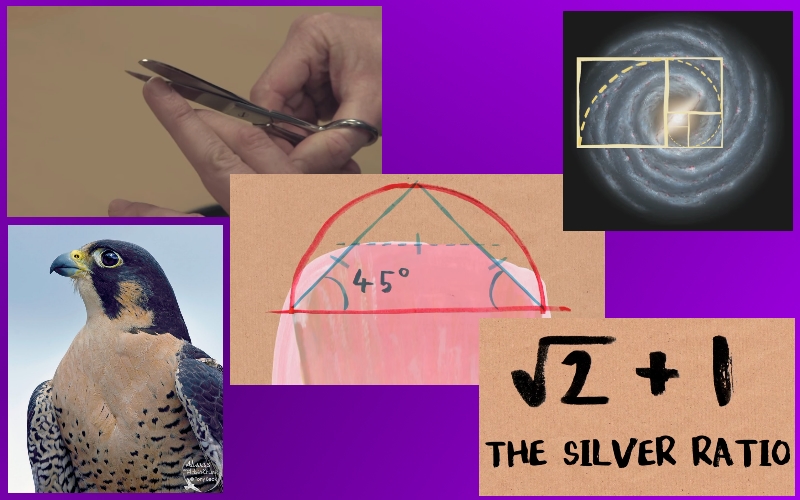
A Zlati rez ni edini, ki je matematično zanimiv. Obstajajo še drugi. Enega recimo najdemo, če si z ravnimi škarjami strižemo nohte. To naredimo pogosto tako, da najprej odrežemo robove pod kotom, nato pa pristrižemo še sredino. Postopek nadaljujemo tako dolgo, da dobimo lepo zaobljen noht. Razmerje med polmerom krožnega loka nepristriženega in pristriženega nohta je √2+1. Sliši se dokaj nenavadno toda zadeva je matematično tako zanimiva, da ima svoje ime – Srebrni rez. In tudi ta je zastopan z nečim, kar je podobno Fibonaccijevemu zaporedju. Dobimo ga podobno kot Fibonaccijevo, le da drugo število najprej podvojimo. Začnemo torej z 0 in 1, enko podvojimo in ji dodamo nič. Dobimo 2. Nato 2 podvojimo in prištejemo 1 in dobimo 5. In tako naprej, da dobimo 0, 1, 2, 5, 12, 29, 70, 169… Zaporedje, ki ga dobimo, se imenuje Pellovo zaporedje oziroma Pellova števila.

Kaj pa ta števila oziroma razmerje pomeni v praksi? Jih prav tako najdemo v naravi, arhitekturi, glasbi in še kje? Pravzaprav niti ne oziroma neprimerno manj, je pa matematično prav tako zanimiv, posebej zato, ker je nekakšne znak oziroma indikator, da za Zlatim rezom obstaja še kaj.

In kaj pomenijo vsi tile rezi grafično? Gremo po vrsti. Vzemimo, da imamo pravokotnik, katerega razmerja stranic so skladna z Zlatim, Srebrnim, Bronastim in še kakšnim rezom. Ali obstaja kakšno pravilo oziroma povezava med njima? Pa si poglejmo:

Zlati rez: če iz pravokotnika izrežemo največji možni kvadrat, bo preostali pravokotnik imel stranice prav tako v razmerju zlatega reza.
Srebrni rez: če iz pravokotnika izrežemo DVA največja možna kvadrata, bo preostali pravokotnik imel stranice prav tako v razmerju srebrnega reza.
Bronasti rez: če iz pravokotnika izrežemo TRI največje možne kvadrate, bo preostali pravokotnik imel stranice prav tako v razmerju bronastega reza.

Vidite, kam pes taco moli? Je mogoče zapisati celo neko splošno formulo kovinskega razmerja reda n? Je. Iz primerov sledi, da v pravokotniku pri nekem razmerju stranic reda n velja, da če od njega odrežemo n kvadratov, bo preostali pravokotnik imel razmerje stranic v enakem razmerju.

In kaj nam dajejo vsi ti rezi? Njihova najpomembnejša lastnost je, da opisujejo tako imenovane logaritmične spirale. Te so pomembne zato, ker nam med drugim omogočajo izdelavo matematičnih opisov dogajanja v naravi, pa naj gre za morske školjke, semena v sončnici, let sokola selca ali vrtinčenje Mlečne ceste. Marsikaj od tega se pripisuje Zlatemu rezu, a ni čisto tako.

Več o srebrnem rezu in ostalih kovinskih rezih v spodnjem videu kanala Numberphile.


Vir: Numberphile