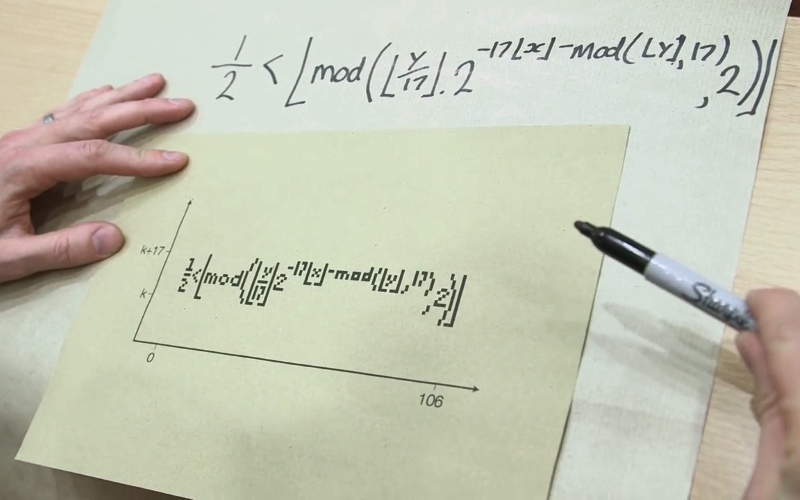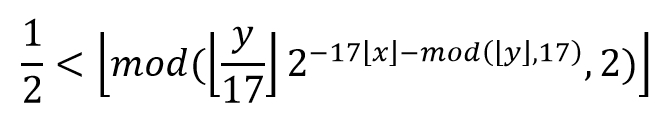
V primeru, da niste ravno matematični navdušenec potem vam bosta v enačbi vsaj dve oznaki precej tuji – oglati oklepaj brez zgornjega »ogla« in oznaka »mod«. Tisti oklepaj je funkcija, ki se imenuje spodnji celi del (ang. floor), njen rezultat pa je največje celo število, ki je manjše ali enako izrazu, ki sledi. Če bi izraz v oklepaju dal vrednost 3,9, bi funkcija dala rezultat 3, če bi bil rezultat -3,1, pa -4 (največje celo število, ki je manjše od tega). Kaj pa »mod«? To pa je funkcija, ki kot rezultat daje ostanek pri deljenju dveh števil. Recimo mod (11,3)=2 ker je 11/3=3 (ostane 2).
Če bi tole čudno formulo šli izrisovati v grafu, bi na določenem mestu v njem dobili tole:
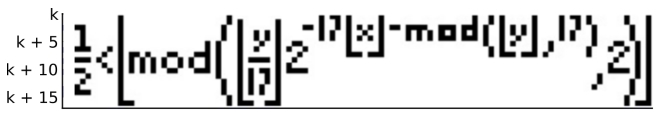
Dobili bi torej - formulo samo. No ja, z malo »švindlanja«, saj je na sliki prikazan le del funkcije, ki se nahaja v okolici števila K. In kje je tale K? Huh, zelo daleč oziroma visoko - v primeru te slike je K namreč kar 543-mestno število. Pa še nekaj je zanimivo – slika odvoda te funkcije je prav tako Tupperjeva enačba, le da je zapisana tako, kot če bi original zavrteli za 90 stopinj v smeri urinega kazalca.
Se vam zdi tole nenavadno? Počakajte, ni še konec. Tupperjeva samoreferenčna formula namreč ne opisuje le samo sebe ampak opisuje, no ja, več ali manj vse. Gre namreč za skupek neskončnega števila »pravokotnikov«, velikih 106 x 17 točk, v katerih je lahko vse, kar si zamislimo, le dovolj visoko v grafu moramo iskati.
Kako je to mogoče? Tupperjeva samoreferenčna enačba je pravzaprav neka splošna metoda, s katero je mogoče dekodirati bitno sliko, shranjeno v konstanti K, to konstanto pa je mogoče definirati po določenih pravilih. Ta pravila lahko vsebujejo načrt, kako izrisati karkoli (dvobarvnega), med drugim seveda tudi izris same sebe. Ali pa izris same sebe, a delno odgriznjene zaradi Pac Mana.
Več v spodnjem videu.
Vir. Numberphile