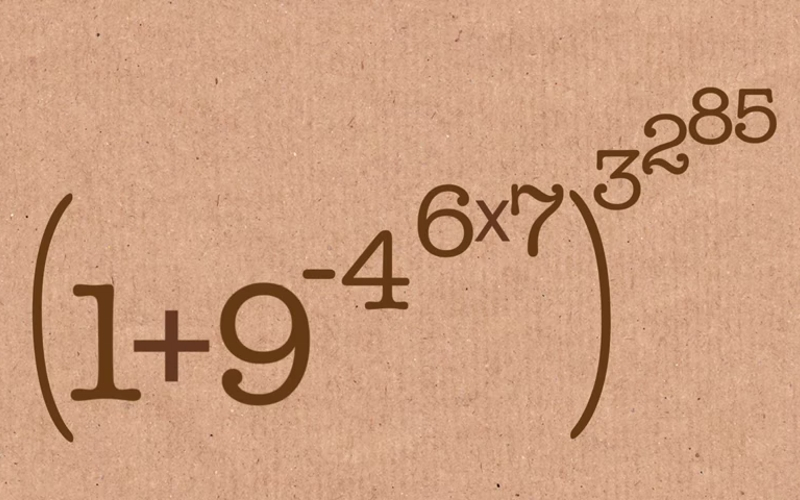Nenavadna formula

Matematiki se seveda radi igrajo s števili. Ena od zabav je tudi raziskovanje tako imenovanih panštevilskih izrazov. To so izrazi, pri čemer lahko gre tako za števila kot za enačbe, v katerih so zastopana vsa števila od 1 do 9 (včasih tudi 0), pri čemer se vsako pojavlja le enkrat. Nekaj teh izrazov je dokaj zanimivih. Recimo število 381.654.729. Zakaj je zanimivo? Zato ker je prvih n števil v njem deljivo z n – 3 je deljivo z 1, 38 z 2, 381 s 3, 3816 s 4 in tako naprej.

Obstajajo pa tudi zanimive enačbe. Recimo ta, ki jo vidite na naslovni sliki in ki jo je leta 2004 »našel« možak z imenom Richard Sabey. Če jo pogledamo, vidimo, da gre res za panštevilski izraz, saj so v njej vsa števila od 1 do 9, so pa izredno nenavadno razporejena. A s tem nenavadnosti še ni konec. Če enačbo rešimo dobimo:

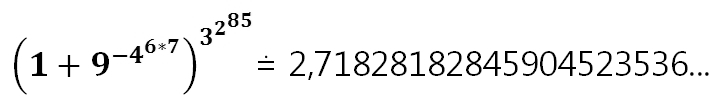
Se vam rešitev zdi kaj znana? Se spomnite Eulerjevega števila »e« iz srednje šole? Rešitev te formule je približno »e«. Kako približno? Zelo, saj je natančnost kar 18 trilijonov trilijonov decimalnih mest (18 in potem še 24 ničel oziroma števk).

In kako je Sabey prišel do formule? Podrobnosti so oglejte v spodnjem videu YouTubovega kanala Numberphile.


Vir: Numberphile