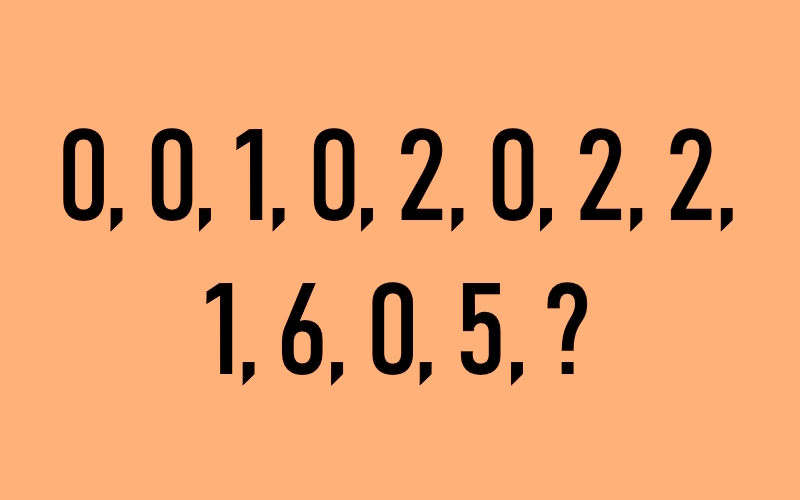Zapisano zaporedje ima prav posebno ime. Imenuje se Van Eckovo zaporedje po Nizozemcu z imenom Jan Ritsema van Eck, ki si ga je izmislil kakih 15 let nazaj. In kako dobimo števila v zaporedju?
Tako, da zapišemo, koliko mest nazaj smo neko število nazadnje videli. V praksi bi bilo to vodeti takole:
- začnemo z 0, saj na začetku še nismo ničesar videli,
- ker števila 0 do sedaj še nismo videli, je naslednje število spet 0,
- če sedaj pogledamo tole drugo ničlo ugotovimo, da smo jo videli en korak oziroma eno mesto nazaj, zato je naslednja vrednost 1,
- enice do sedaj še nismo videli, zato sledi 0,
- ničlo smo videli, tokrat dve mesti nazaj, zato sledi število 2,
- dvojke še ni bilo, zato spet sledi 0,
- zadnja ničla je bila dve mesti nazaj, zato 2,
- število 2 smo nazadnje videli dve mesti nazaj, zato spet sledi 2,
- zadnjo dvojko pred tole zadnjo smo videli en korak nazaj, zato sledi 1,
- enico smo nazadnje videli šest mest nazaj, zato sledi število 6
- itn…
Van Eckovo zaporedje je mogoče sicer res zanimivo, a je le eno od več sto tisoč zaporedij, objavljenih v Spletni enciklopediji celoštevilskih zaporedij (On-Line Encyclopedia of Integer Sequences – OEIS). Da, takšna enciklopedija dejansko obstaja, njen avtor pa je prav prej omenjeni Neil Sloane. Neil je začel celoštevilska zaporedja zbirati leta 1964 kot študent matematike na univerzi Cornell. Leta 1973 je njegova zbirka vsebovala 2372 takšnih zaporedij in objavil jih je v knjigi z naslovom The Handbook of Integer Sequences. Z zbiranjem seveda ni nehal in do leta 1996 se jih je tako zbralo že več kot 10.000. Ker objava takšnega števila zaporedij v papirni obliki ni več smiselna, se je Sloane odločil, da jih objavi v spletu, ki je takrat ravno pošteno zaživel in k sodelovanju povabi ves svet.
In odziv je bil daleč nad pričakovanji. V naslednjih petnajstih letih je baza rasla s hitrostjo 10.000 do 18.000 zaporedij na leto in je Sloan sam ni mogel več vzdrževati. Zato je leta 2009 ustanovil neprofiten sklada, ki zbira denar za to, da zadeva lahko domuje pri komercialnem ponudniku gostovanja spletnih strani, za vsebino pa je pričel skrbeti veččlanski uredniški odbor. Baza OEIS, ki je med drugim na voljo tudi v slovenščini, je lani marca presegla 300.000 zaporedij, kar je res ogromno.
Vas zanima, kako nadaljevati neko zaporedje, pa ne najdete vzorca? Znane številke vpišite v bazo OEIS in ta vam bo vrnila odgovor. Tudi več odgovorov…
Kdo bi si mislil, da je lahko nekaj, kar se imenuje celoštevilska zaporedja, deležno toliko pozornosti…
Vir: OEIS