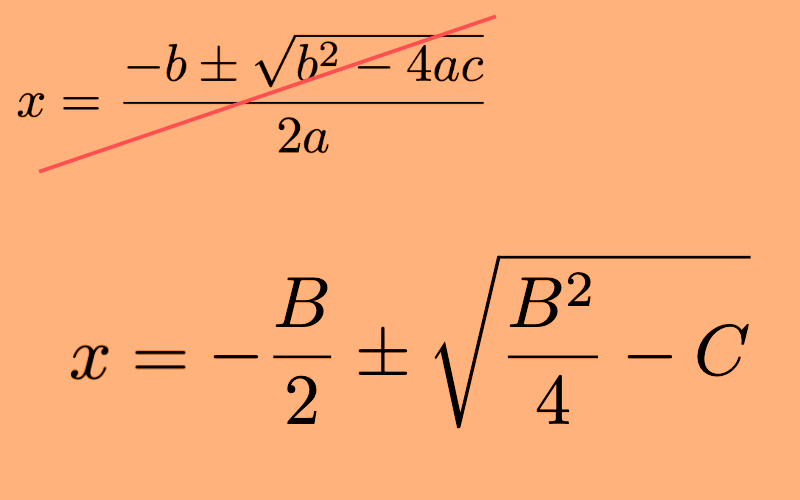Kvadratna enačba »po novem«

Se spomnite kvadratnih funkcij in enačb iz srednje šole, kjer ste ničle oziroma presečišča funkcije z osjo x iskali v lažjih primerih po Viettovem pravilu, pri težjih pa po metodi z diskriminanto? Vas malce spomnimo?

Če imamo kvadratno enačbo v obliki x²+bx+c=0, smo razcep po Viettovem pravilu iskali tako,da smo iskali števili, katerih vsota je bila število b, produkt pa število c. V primeru x²-4x-12=0 sta ti dve števili -6 in 2, saj je -6+2= -4 in -6x2= -12 in razcepljena enačba se glasi (x+6)(x-2)=0.

Če je enačba malce bolj zoprna in ima tudi parameter a ali pa sta b in c vrednosti, kjer rešitve ne moremo kar »videti«, se pač uporablja tista znana formula, ki se je verjetno še spomnite:

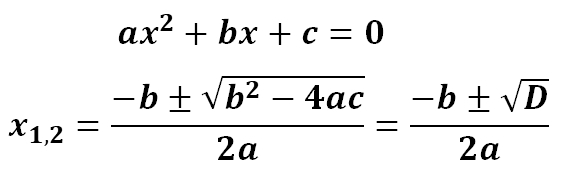
Ko ste vanjo vstavili a, b in c ste dobili iskani dve rešitvi.

No, matematik Po-Shen Loh z ameriške univerze Carnegie Mellon, je sedaj, kakih 4000 let po tem, ko so Babilonci »izumili« prejšnjo metodo, našel še eno, ki je dokaj preprosta, saj omogoča določanje rešitev le v pomočjo koeficientov b in c (če obstaja tudi a, pač celotno enačbo delimo z njim in dobimo nova b in c). Enačba se glasi:

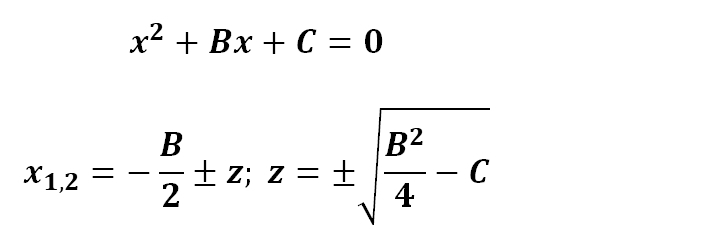
Vidimo, da sta v njej le koeficienta B in C in da je malce manj zoprna od »originala«. Pa jo preverimo. Vzemimo kvadratno enačbo: 2x²-8x-24=0 in jo poskusimo rešiti. Ker je v njej koeficient a, se ga najprej znebimo tako,da  enačbo delimo z njim. Ostane nam x²-4x-12=0, kar je enak primer kot prej pri Viettovem pravilu. Koeficienta B  in C sta torej -4 in -12. Če ju sedaj vstavimo v »novo« enačbo, lahko kaj hitro izračunamo obe rešitvi.

In kako je Po-Shen Loh prišel do te rešitve? Pravzaprav na dokaj preprost način. Celoten dokaz oziroma postopek si lahko ogledate na tej povezavi, na tem mestu pa le njegova »filozofija«. Pri Viettovem pravilu smo rekli, da iščemo dve števili (x₁ in x₂), katerih vsota bo koeficient B. Kaj pa povprečje teh dveh števil? To je seveda –B/2. In kje leži to povprečje? Po definiciji med vrednostma x₁ in x₂, od njiju pa je oddaljeno za nek z. To pomeni, da sta rešitvi enačbe tudi x₁=-B/2+z in x₂=–B/2-z. Po Viettovem pravilu pa velja, da mora biti produkt rešitev enak koeficientu C, torej moramo prejšnji dve rešitvi zmnožiti C=(-B/2+z)( -B/2-z) = (-B/2)²-z². Od tu lahko z malo premetavanja izrazimo z in dobimo omenjeno novo formulo.

Je takšno računanje res lažje? Vzemimo naš primer x²-4x-12=0 Vidimo, da je –B/2=-(-4)/2=2, sedaj moramo samo še izračunati z, kar je iz omenjenih številk dokaj preprosto in dobimo 4. To sedaj prištejemo in odštejemo od 2 in dobimo rešitivi. Res je lažje…

Vir: MIT Technology Review