Rimska števila obsegajo »števke« I, V, X, L, C, D M, ki v arabskem zapisu pomenijo 1, 5, 10, 50, 100, 500 in 1000 in števila so se, kot zagotovo veste, zapisovala s kombinacijo teh števk. To pa je bilo precej nepraktično, še bolj nepriročno pa je bilo to, da zaradi več različnih možnosti zapisa istega števila ni bilo enovitega načina. Kot lahko vidite na spodnji sliki, je število 999 z rimskimi števili mogoče zapisati na vsaj štiri načine:

Drugi problem je da rimska števila zasedajo veliko prostora. Število 1000 je sicer res M, a le ena manj, torej 999, je že čudnih CMXCIX. A to še nekako gre. Recimo število 3888 je z MMMDCCCLXXXCII že skoraj roman…
Naslednja težava je, da v rimskih številih ni ničle. No, ja, pravzaprav je, saj so poznali izraz »nulla«, ki je pomenila »nič« in nekdo se je celo spomnil in ji dal oznako N, kar pa se »ni prijelo«, saj so nekateri N uporabljali kot »bližnjico« za število 90.
Vse našteto več ali manj že vemo. Manj znano pa je, da so v rimskih številkah obstajali tudi recimo ulomki. Sicer »bolj tako«, so pa. Obstajal je recimo S, ki je bil zapis za 6/12, a se je uporabljal tudi za 1/2. Dvanajstine so bile uporabljene zato, ker je število 12 deljivo s toliko različnimi števili – 1, 2, 3, 4, 6 in seveda 12, vendar je imelo le 6/12 svojo črkovno oznako, manjše vrednosti pa točke oziroma pike:

Ti ulomki so bili seveda uporabni tudi v kombinaciji s »klasičnimi« števili. Število 4 ½ se je recimo glasilo IVS, kar niti ni hudo zoprno, mar ne?
Še ena zanimiva posebnost je tako imenovani Vinculum. Gre za način zapisa zelo velikih števil. Če bi hoteli recimo zapisati število 10.000 na običajen način, bi morali zapisati 10 črk M, kar je seveda zelo nepraktično in neberljivo. Zato so si omislili zapis z nadčrtajem, podobno kot recimo zdaj označujemo povprečje ali ponovitev decimalke. Omenjeno število 10.000 se recimo zapiše kot X̅, kar pomeni, da X, torej 10, množimo s 1000. A ker brez zapletanja stvari očitno tudi tu ni šlo, je 10.000 mogoče zapisati tudi kot M med dvema navpičnicama, torej |M|, kar pomeni, da je število M, torej 1000, potrebno množiti z 10. Število 10.000 je torej 1000 x 10 ali pa 10 x 1000, kar matematično seveda drži, zapis pa je dokaj zoprn, mar ne... Zdaj pa si zamislite, da je bilo to treba seveda kombinirati z vsem drugim prej zapisanim. A še ni konec...
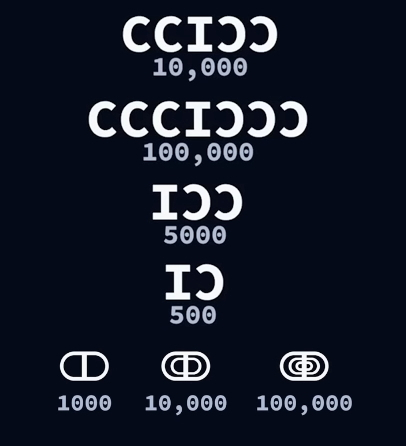
Poleg vinculuma so bili v uporabi tudi apostrofi ali slovensko opuščaji, ki pa so imeli malce drugačno nalogo. Število 10.000 mogoče zapisati tudi s pomočjo štirih paroma zrcalno zapisanih C-jev, med katerimi je bila enica oziroma I, 100.000 šestih, večjih števil kot to pa niso našli zapisanih nikjer. Z zrcalnimi C-ji je bilo mogoče zapisati tudi število 5000, kjer sta se uporabila le dva zrcalna C-ja, pri število 500 pa le eden. Ker je bilo vse skupaj seveda kaotično, so za 1000, 10.000 in 100.000 uporabljali »združene« simbole, kot jih lahko vidite na spodnji sliki, s čemer pa, roko na srce, kaosa niso ničkaj zmanjšali...
Je potem čudno, da so hindujska/arabska tako hitro zavzela svet?
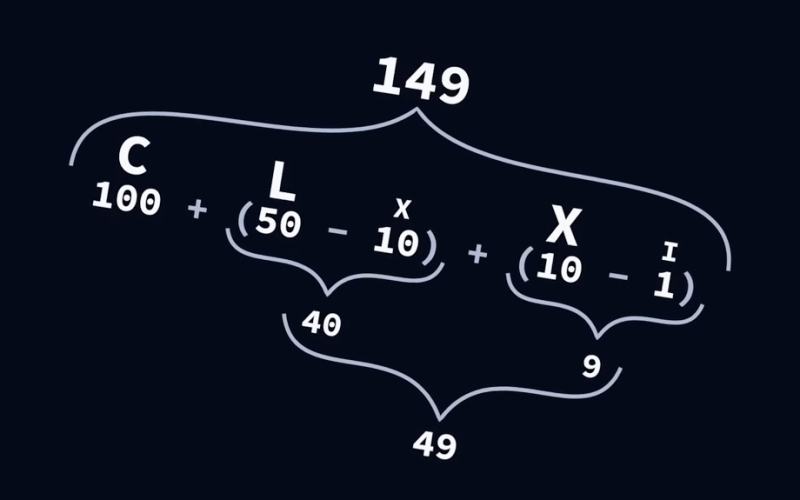
OPOMBA: Število 149 na naslovni sliki se pravilno seveda zapiše z CXLIX in ne CLXXI, kot bi se zdelo. Na sliki gre le za ponazoritev filozofije odštevanja.
▪