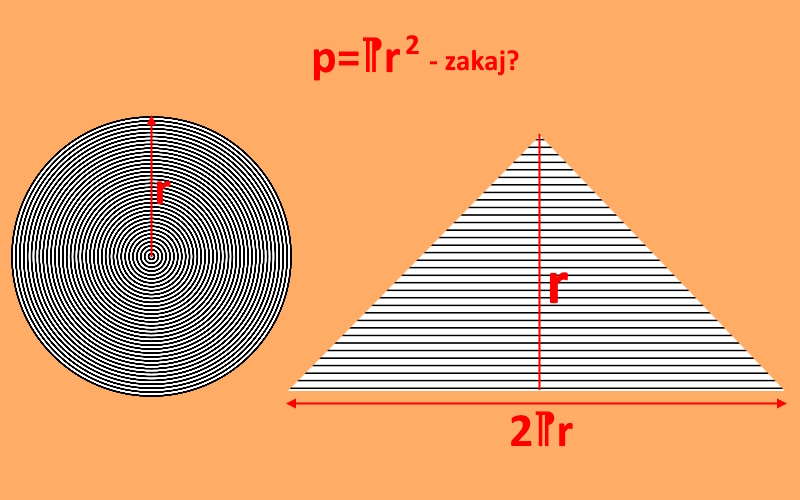
Zamislite si, da je krog sestavljen iz neskončnega števila koncentričnih krožnic, kot je to na naslovni sliki. Če zdaj vzamemo vsako krožnico, jo razpremo in jih zložimo eno na drugo, dobimo trikotnik, katerega osnovnica je dolga 2πr (obseg najdaljšega kroga), višina pa r. Ker smo uporabili izključno »elemente« kroga, bo ploščina tega trikotnika enaka ploščini kroga. Ploščino trikotnika pa znamo izračunati, mar ne? Formula je dokaj preprosta, saj moramo zmnožiti višino in polovico osnovnice (p= (o·v)/2). Če to zdaj uporabimo v primeru kroga, kjer je osnovnica 2πr, višina pa r vidimo, da se formula glasi:
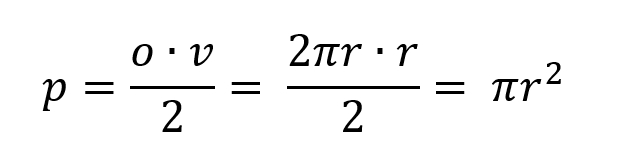
In kot vidite, smo dobili enak rezultat kot s »torticami«… ▪